티스토리 뷰
https://leetcode.com/problems/range-sum-of-bst/
Range Sum of BST - LeetCode
Level up your coding skills and quickly land a job. This is the best place to expand your knowledge and get prepared for your next interview.
leetcode.com
Given the root node of a binary search tree, return the sum of values of all nodes with value between L and R (inclusive).
The binary search tree is guaranteed to have unique values.
Note:
- The number of nodes in the tree is at most 10000.
- The final answer is guaranteed to be less than 2^31.
해석
이진트리의 루트노드가 주어지면, L 과 R 값 사이의 값을 가진 모든 노드의 총합을 반환하라
바이너리 트리는 각각 고유값으 갖는다
Note:
- 1. 트리의 노드 갯수는 1000개 미만이다.
- 2. 결과 값은 2^31 보다 작다.
Example 1.
Input: root = [10,5,15,3,7,null,18], L = 7, R = 15 Output: 32
Example 2.
Input: root = [10,5,15,3,7,13,18,1,null,6], L = 6, R = 10 Output: 23
기본지식
바이너리 트리 (이진트리)
- 각 노드가 최대 두개의 자식 노드를 갖는 트리
- 위키피디아 '이진 트리'[링크] 참고
예제 해석
Example 1.
주어진 조건의 트리 모습은

그 중, 7 이상 15 이하의 값을 갖는 노드는 [7 , 10 , 15]
즉, 노드의 값의 합은 [7 + 10 + 15] = 32
Output : 32
Example 2.
주어진 조건의 트리 모습은
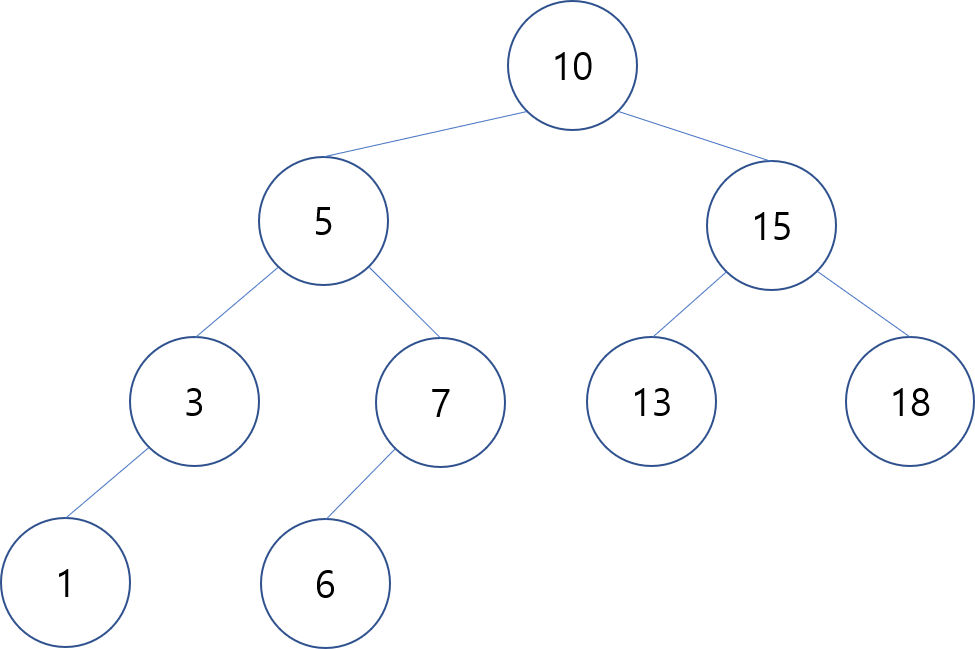
그 중, 6 이상 10 이하의 값을 갖는 노드는 [6 , 7 , 10]
즉, 노드의 값의 합은 [6 + 7 + 10] = 23
Output : 23
솔루션 Solution
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public int rangeSumBST(TreeNode root, int L, int R) {
//존재하지 않는 노드
// 0을 반환한다
if(root == null) return 0;
// 좌우측 자식노드로부터 반환받은 값에
// 자신의 값이 조건에 일치할경우 자신의 값을, 아닐경우 0 을 더해 최종 반환한다
return ((root.val >= L && root.val <=R)? root.val : 0) + rangeSumBST(root.left,L,R) + rangeSumBST(root.right,L,R); //자신의 값이 조건에 맞을 경우 좌우 자식노드에서 탐색해 합산해 온 값에 더하여 반환한다
}
}
문제 풀이의 핵심은 이진탐색과 재귀호출에 있다.
이진탐색은 주어진 노드의 좌/우 자식 노드로 이동하며 탐색하게된다
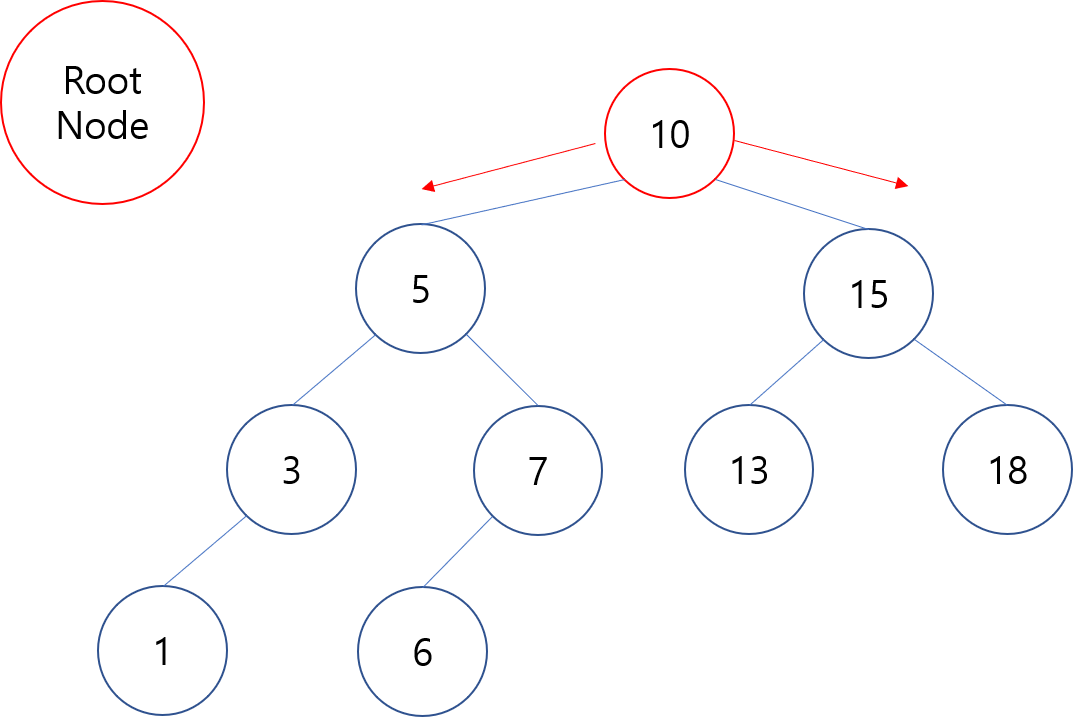
Step 1. Root Node 의 좌/우 자식노드를 탐색한다.
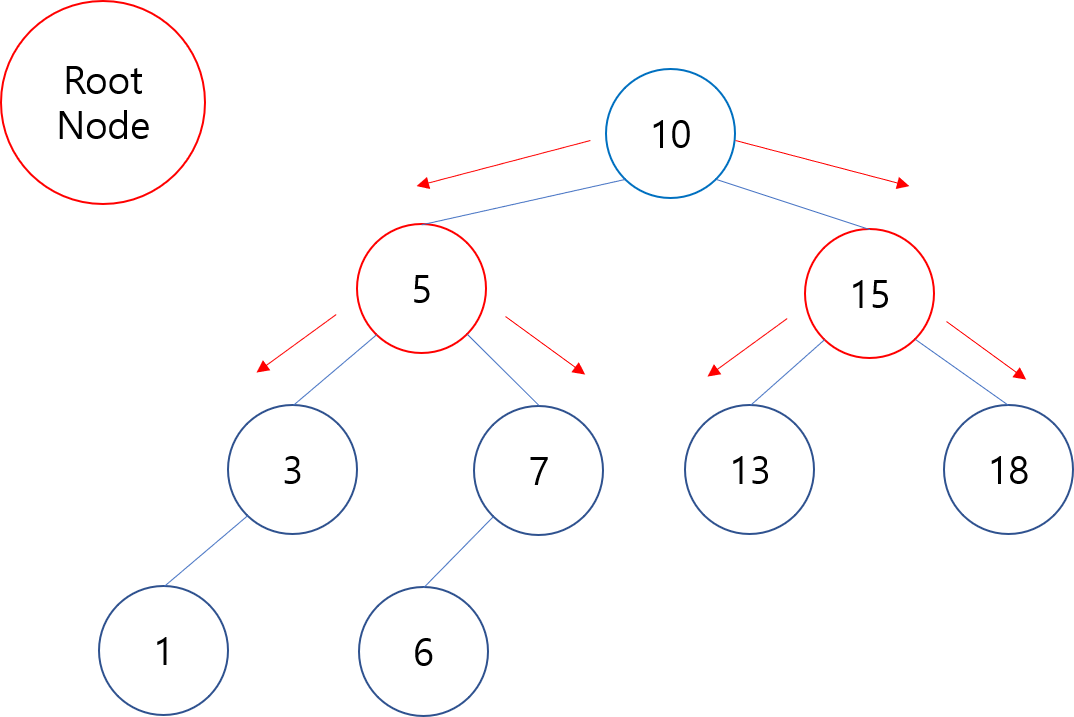
Step 2. 기존 Root Node의 좌/우 노드는 각각 Root Node가 되며, 자신의 좌/우 자식노드를 탐색한다.
Step1과 Step2는 RootNode가 부모노드에서 자식노드로 변경된 차이만 있으며, 자신의 좌/우 자식노드를 탐색한다는 것은 동일하다.
즉, 탐색방법은 동일하기때문에 재귀호출을 사용하면 된다.
void binarySearch (TreeNode root){
//좌측 자식 노드 탐색
binarySearch(root.left);
//우측 자식 노드 탐색
binarySearch(root.right);
}
문제에서는 조건에 맞는 노드 값의 합을 요구하고 있다.
RootNode는 자신의 값이 조건에 맞는지 판단하면 되며, 그 이하 노드들은 좌/우 자식노드에게 탐색하도록 한다.
RootNode는 자신의 값과 좌/우 자식노드 탐색 결과를 합산해 최종 반환하면 된다.
'LeetCode' 카테고리의 다른 글
| [LeetCode] 1008. Construct Binary Search Tree from Preorder Traversal (0) | 2019.06.10 |
|---|---|
| [LeetCode] 804. Unique Morse Code Words (0) | 2019.06.06 |
| [LeetCode] 1021. Remove Outermost Parentheses (0) | 2019.06.04 |
- Total
- Today
- Yesterday
- unit test
- 안드로이드 테스트
- android compose
- AOS
- ViewCompositionStrategy
- compose ui
- 안드로이드
- 안드로이드 커스텀 버튼
- android test
- 컴포즈 초기화
- Unit
- 알고리즘 풀이
- 안드로이드 컴포즈
- button padding
- 안드로이드 종속성 주입
- 커스텀 버튼
- Leetcode
- 안드로이드 유닛 테스트
- 안드로이드 단위 테스트
- 유닛 테스트
- 코딩테스트
- 유닛테스트
- 알고리즘
- 테스트
- 구글
- Android
- androud hilt
- android custom button
- android unit test
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
